Reference:
http://www.math.uiuc.edu/~r-ash/CV/CV1.pdf
http://en.wikipedia.org/wiki/Cauchy%E2%80%93Riemann_equations
http://mathworld.wolfram.com/Cauchy-RiemannEquations.html
1. If z = a + bi, then a is called the real part of z, written a = R ez, and b is called the
imaginary part of z, written b = Imz. The absolute value or magnitude or modulus of z
is defined as (a2 +b2)1/2.
2. A complex number with magnitude 1 is said to be unimodular.
3. An argument of z (written arg z) is defined as the angle which the line segment from (0, 0)
to (a, b) makes with the positive real axis.
4. to a multiple of 2π.
If r is the magnitude of z and θ is an argument of z, we may write
z = r(cos θ + i sin θ)
5.
The Cauchy–Riemann equations on a pair of real-valued functions u(x,y) and v(x,y) are the two equations:
- (1a)

and
- (1b)

Typically
u and
v are taken to be the
real and
imaginary parts respectively of a
complex-valued function
f(
x + i
y) =
u(
x,
y) + i
v(
x,
y).
6.
If 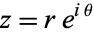 , then the Cauchy-Riemann equations become
, then the Cauchy-Riemann equations become
7.
If  and
and  satisfy the Cauchy-Riemann equations, they also satisfy Laplace's equation in two dimensions, since
satisfy the Cauchy-Riemann equations, they also satisfy Laplace's equation in two dimensions, since
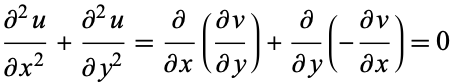 |
(20)
|
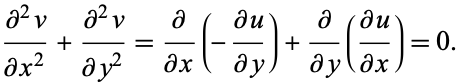
8. An analytic signal is a signal with no negative-frequency components
9. A function is analytic if and only if it is equal to its Taylor series in someneighborhood of every point.
10. Any polynomial (real or complex) is an analytic function. This is because if a polynomial has degree n, any terms of degree larger than nin its Taylor series expansion will vanish, and so this series will be trivially convergent. Furthermore, every polynomial is its own Maclaurin series.
11.
- The exponential function is analytic. Any Taylor series for this function converges not only for x close enough to x0 (as in the definition) but for all values of x (real or complex).
Typical examples of functions that are not analytic are:
- The absolute value function when defined on the set of real numbers or complex numbers is not everywhere analytic because it is not differentiable at 0. Piecewise defined functions (functions given by different formulas in different regions) are typically not analytic where the pieces meet.
- The complex conjugate function
 is not complex analytic, although its restriction to the real line is the identity function and therefore real analytic. is not complex analytic, although its restriction to the real line is the identity function and therefore real analytic.
12. In mathematics, the Laurent series of a complex function f( z) is a representation of that function as a power series which includes terms of negative degree. It may be used to express complex functions in cases where a Taylor series expansion cannot be applied.
|





 is not complex analytic, although its restriction to the real line is the identity function and therefore real analytic.
is not complex analytic, although its restriction to the real line is the identity function and therefore real analytic.